Long-term Forecasting with TiDE: Time-series Dense Encoder - 论文阅读
Date:
论文: 一种名为 TiDE(时间序列密集编码器)的模型,用于长期预测时间序列数据 论文地址:https://arxiv.org/pdf/2304.08424
一.模型介绍
1.1 前言
最近的工作表明,在长期时间序列预测中,简单的线性模型可以优于几种基于Transformer的方法。受此启发,文章提出了一种基于多层感知器(MLP)的编码器-解码器模型,即时间序列密集编码器(TiDE),用于长期时间序列预测,该模型具有线性模型的简单性和速度,同时能够处理协变量和非线性依赖关系。理论上,文章证明了该模型的线性类似物可以在某些假设下实现对线性动力系统(LDS)的近最优错误率。经验上,该方法可以在流行的长期时间序列预测基准上匹配或优于以前的方法,同时比最好的基于Transformer的模型快5-10倍。
这篇论文的主要贡献包括:
- 提出了用于长期时间序列预测的时序密集编码器(Time-series Dense Encoder,TiDE)模型架构。TiDE使用密集多层感知器(MLP)对时间序列的过去和协变量进行编码,然后使用密集MLP对时间序列和未来的协变量进行解码。
- 对模型的线性类似物进行了分析,并证明了当线性动力系统(LDS)的设计矩阵的最大奇异值远离1时,该线性模型可以达到接近最优的错误率。在模拟数据集上进行了实证验证,其中线性模型优于LSTM和Transformer。
- 在流行的真实世界长期预测基准上,与基于神经网络的先前基准相比,模型实现了更好或相似的性能(在最大数据集上降低了10%以上的均方误差)。同时,与最佳基于Transformer的模型相比,TiDE在推理方面快5倍,训练方面快10倍以上。

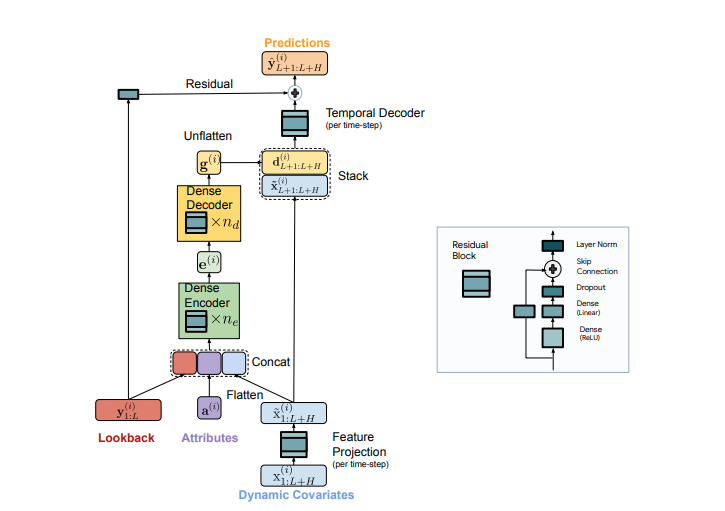
1.2 模型结构
该模型专注于解决多元长周期时间序列预测任务。整个TiDE模型结构都由MLP组成,解决了之前线性模型无法建立预测窗口与历史窗口之间非线性关系的问题,同时也解决了无法有效建立外部变量的问题。
模型的核心基础组件是残差块,由一个Dense+RLU层、一个Dense线性层和一个Add&Layernorm组成。TiDE的其他组件都是在这个基础组件上搭建而成的。整体上,模型可以分为四个部分:特征投影、密集编码器、密集解码器和时序解码器。
特征投影将外部变量映射到一个低维向量,这是通过使用Residual Block实现的,主要目的是降低外部变量的维度。
密集编码器部分将历史序列、属性信息以及外部变量映射的低维向量拼接在一起,并使用多层Residual Block对其进行映射,最终得到一个编码结果 e 。
密集解码器部分将编码结果 eee 使用同样的多层Residual Block映射成 g ,并将 g 重塑成一个 [p,H] 的矩阵。其中 HHH 对应的是预测窗口的长度, p 是解码器输出维度,相当于预测窗口每个时刻都得到一个向量。
时序解码器将上一步的 g 和外部变量 x 按照时间维度拼接到一起,使用一个Residual Block对每个时刻的输出结果进行映射。在此之后,历史序列的直接映射结果被加入残差连接中,得到最终的预测结果。
二、理论和实验分析
2.1 理论分析:
正式定义一个线性动力系统(LDS)如下,
定义2.1:一个线性动力系统(LDS)是将输入向量序列 X1, X2, … , Xt 属于 Rn 映射到输出(响应)向量序列 y1, …, Yt 属于 Rm 的一种形式
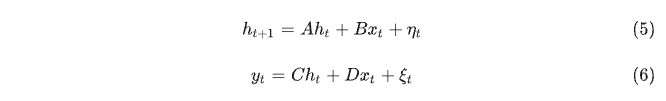
其中 h0,…,ht 属于Rd 是隐形状态的序列,A,B,C,D是相应维度的矩阵,Xts 可以被视为时间序列Yt的协变量。
给定一个参数Q = (A,B,C,D, ho = 0)的LDSL
定义2.2:(LDS预测器)
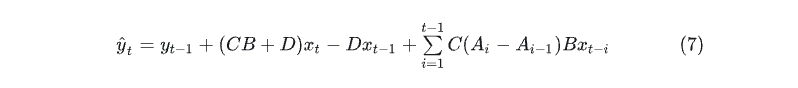
命题2.3:学习LDS的自回归泛化界
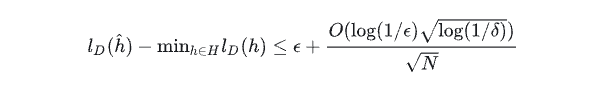
上述结果表明,具有短回顾窗口的线性自回归预测器与最佳LDS预测器具有竞争力,其中转移矩阵A的最大特征值严格小于1。
2.2 实验分析:
在由线性动力系统生成的合成数据集上评估了几个模型。转移矩阵A是一个30×30维的Wishart随机矩阵,归一化的算子范数为0.95。状态转移中的噪声 Nt遵循30维高斯分布。每个时间步的输入xt遵循5维标准高斯分布,这对模型来说是可观察的。最后,在线性动力系统中添加了6种不同周期性的季节性,通过添加余弦信号作为输入,但隐藏在预测模型之外。生成了4个不同的时间序列,它们共享相同的模型参数、输入 Xt和季节性输入,唯一不同的是状态转移中的随机性。把回看窗口设置为长度320,并且视野也是长度320。对于每个时间序列,使用前1640个步骤进行训练,接下来的740个步骤进行验证,最后的740个步骤进行测试,这产生4000个训练样本、400个验证样本和400个测试样本。
在合成数据集上评估了三种模型:线性模型、长短时记忆(LSTM)和Transformer。线性模型是回溯窗口中的历史与未来之间的直接线性映射。使用一层维度为128的LSTM。对于Transformer,使用两层自注意力层,维度为128,结合一层具有128个隐藏单元的隐藏层的馈送前馈网络。

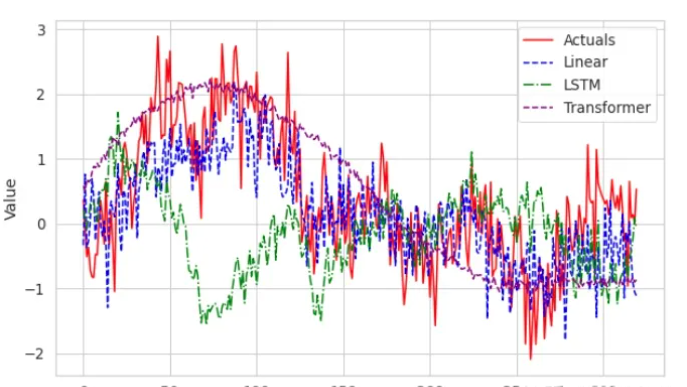
对于所有模型,报告的是每种设置的3个独立运行结果的平均值和标准差。粗体数字来自于最佳模型或统计意义上看最佳模型在两个标准误差区间。LSTM和Transformer模型的实际值(地面真实)与预测值的对比(图)。可以看到,Transformer捕获了时间序列的低频季节性,但似乎无法利用输入/协变量来预测价值的短期变化,LSTM似乎没有正确捕获趋势/季节性,而线性模型的预测结果最接近真实值,与表1中的指标结果相符。
三、实验结果
3.1 长周期的时间序列预测
文章使用了七个常用的长期预测基准数据集:气象、交通、电力以及4个ETT数据集(ETTh1、ETTh2、ETTm1、ETTm2)。表2提供了一些有关数据集的统计信息。请注意,交通和电力是最大的数据集,每个都有数万个时间序列和数十万个时间点。由于在本节中只对长期预测结果感兴趣,因此省略了较短的时间跨度的ILI数据集。
表2为所有的数据集和方法提供了均方误差(MSE)和均绝对误差(MAE)。对于模型,在每种设置中报告了5次独立运行得出的平均指标。粗体数字代表的是最佳模型或在两个标准误差区间内与最佳模型统计意义相当的结果。
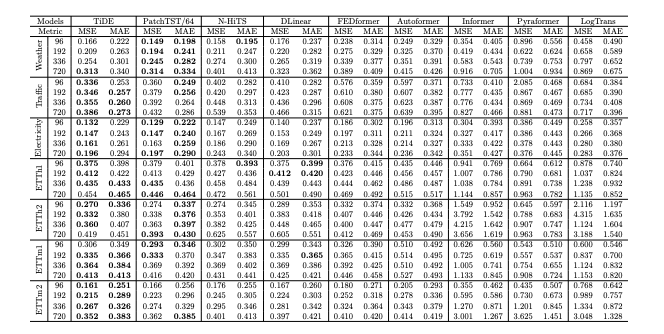
可以看出,TiDE、PatchTST和DLinear在所有数据集中的表现都优于其他基准。此外,在除ETTh1的192时间范围外的所有设置中,模型的表现都显著优于DLinear。这表明模型中额外的非线性是很有价值的。在除Weather之外的所有数据集中,模型的表现要么优于PatchTST,要么与之无统计差异。在Weather数据集中,PatchTST在96-336时间范围内的表现最佳,而模型在720时间范围内的表现最好。在最大的数据集Traffic中,模型在所有设置中都显著优于PatchTST。例如,在720时间范围内,模型的预测在MSE方面比PatchTST高出10.6%。
3.2 训练和预测的效率
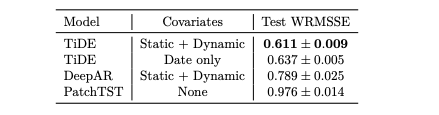
在上一部分中,本文看到TiDE在除Weather以外的所有数据集上,除了PatchTST之外,表现出色或与之相当,同时其在训练和推理时间方面比PatchTST更高效。
本文在实践中展示了这些效果,如图3所示。为了使比较公平,本文使用Autoformer代码库中的数据加载器进行实验,该代码库在所有后续论文中都有使用。本文使用电力数据集,批量大小为8,因为电力数据集具有321个时间序列。每个批次的形状为 8 * 321 * L。随着L从192增加到2880,本文报告了TiDE和PatchTST的一个批次的推理时间和一个训练周期的训练时间。本文可以看到推理时间存在数量级的差异。训练时间的差异更大,PatchTST对回顾时间大小更加敏感。此外,对于 L >= 1440,PatchTST会耗尽内存。因此,本文的模型能够实现更好或类似的准确性,同时比PatchTST更高效和更稳定
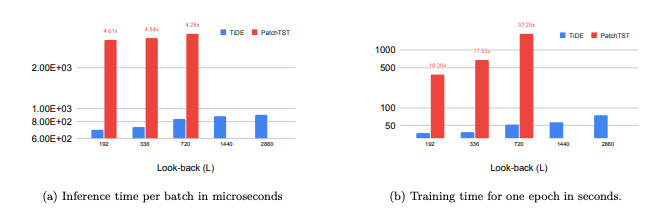
本节中的所有实验均在同一台机器上使用单个NVIDIA T4 GPU进行,该机器具有64个核心的Intel(R) Xeon(R) CPU @ 2.30GHz。
3.3 消融研究
对于未来协变量的适应,使用时间解码器可能是模型中最有趣的组件之一。因此,在本节使用电力数据集的半合成示例来展示该组件的有用性。
本文从一个电力数据集中派生出一个新数据集,其中本文为两种事件添加了数值特征。当发生类型为 A 的事件时,时间序列的值以 [3,3.2] 之间均匀选择的一个因子增加。当发生类型为B的事件时,时间序列的值以 [2,2.2] 之间均匀选择的一个因子减少。只有80%的时间序列受到这些事件的影响,而在此括号内的时间序列ID是随机选择的。有4个数值协变量表明类型 A 和4个表明类型 B 。当类型A事件发生时,类型A协变量从各坐标均值为 [1.0,2.0,2.0,1.0] 、方差为0.1的各向同性高斯分布中抽取。另一方面,在没有类型 A 事件的情况下,类型 A 协变量从各坐标均值为 [0.0,0.0,0.0,0.0] 的各向同性高斯分布中抽取。因此,这些协变量作为事件的噪声指标。对类型 B 的事件和协变量遵循类似的方法,但具有不同的均值。无论何时发生这些事件,它们都会持续24个连续小时。
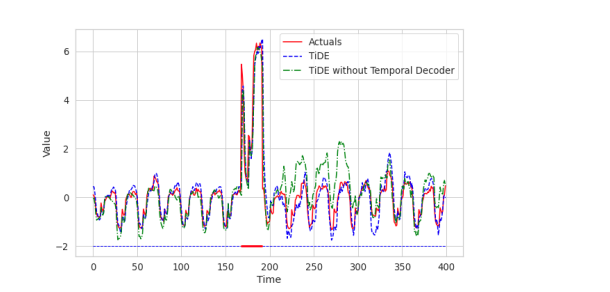
为了证明使用时序解码器可以更快地学习来自协变量的此类模式,本文在修改后的电力数据集上仅进行一次训练后,绘制了具有和不具有时序解码器的TiDE模型的预测结果(图4)。水平线上的红色部分表示A型事件的发生。可以看到,在这段时间内,使用时序解码器具有轻微的优势。但更重要的是,在事件发生后的时间点,没有使用时序解码器的模型可能会偏离轨道,因为它尚未根据没有事件的情况重新调整其过去。即使仅经过一个训练周期,使用时序解码器的模型中这种影响可以忽略不计。
四、结论
本文提出了一种简单的基于多层感知器(MLP)的编码器-解码器模型,该模型在流行的长期预测基准测试中,与以前的神经网络基线匹配或超越了先前神经网络基线的性能。同时,本文的模型比最好的基于转换器的基线快5-10倍。研究表明,至少对于这些长期预测基准测试来说,自注意力可能不是学习周期性和趋势模式的必要条件。本文的理论分析部分解释了为什么会这样,证明了当真实数据是由线性动力系统产生时,线性模型可以达到接近最优的速度。然而,未来的工作有趣的是,通过一些简单的数学模型对时间序列数据的MLP和Transformer进行严格的分析,并可能量化这些架构在不同季节性和趋势水平上的(不利)优势。
